不偏分散の正の平方根は不偏標準偏差でよろしいのか(よろしくない)
記述統計と異なり推測統計は記号・表記や,このタイトルのような話など学ぶ側から眺めると本によって記載が異なるので,謎めいた感あふれる分野に映っていると思います.授業では謎分野にならないよう注意深く臨むのですが,早々に授業を理解する取り組みをあきらめて世の中のソースや友人に頼ってなんとかした学生さんは単位を取得しただけだとしても,社会では統計に見識のある人材と見做されますので,期待外れにならんと良いなと思う今日この頃です.
本題ですが,記述統計では分散の正の平方根を標準偏差としていますが,推測統計においても同様のノリだと,「不偏分散の正の平方根を不偏標準偏差とする」となります.そのような数式を記載をされている本を教科書として用いていたことから,便宜上そのような説明をしたこともあります.非常にわかりやすい本で授業も進めやすかったのですが,他の理由から現在その本は用いておりません.
不偏推定とは一方に偏った推定にならないことですから,不偏分散が偏った推定になっていないのであれば,「不偏分散に基づく標準偏差」(不偏分散の正の平方根)の分布は当然偏るという話です.
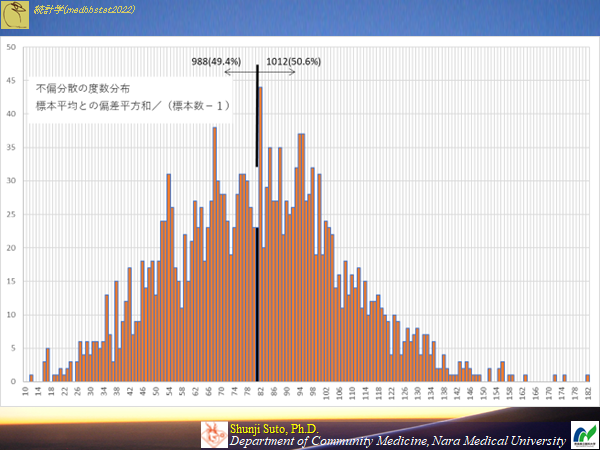
以下は,一様分布のダミーデータを20000用意し,サンプル数2000サンプルサイズ10のデータ(母平均は125.0,母分散は81.0,母標準偏差は9.00)にして求めた不偏分散のヒストグラムです.母分散を中心に偏ることのない推定がされています.
なお不偏分散の期待値は81.1になりました.
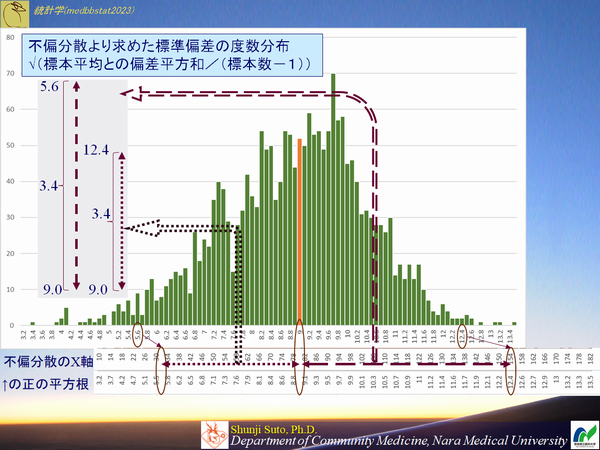
では,「不偏分散に基づく標準偏差」も同様にヒストグラムを作成しました.
「不偏分散に基づく標準偏差」の期待値は8.87になりました.先ほど求めた不偏分散の期待値81.1の正の平方根(9.00)と異なります.母平均周辺のヒストグラムが左右非対称になっています.
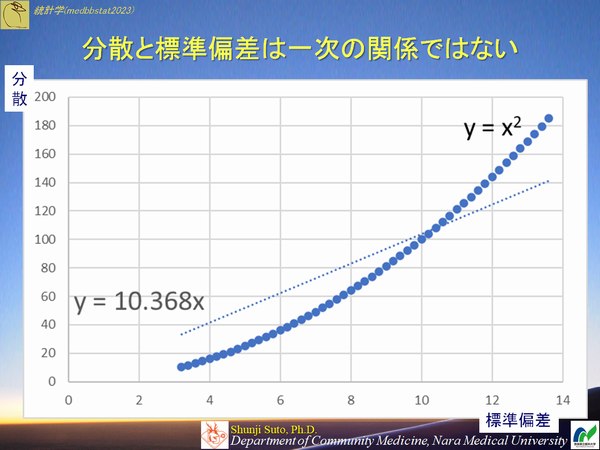
不偏分散の時のX軸を,分散81.0,標準偏差は9.00のところを揃えて表記すると,母平均よりも高い値は圧縮されており,低い値が低い側に間延びしていることがわかります.故に不偏分散と比較すると値が全般的に低い側にシフトしているわけですが.両者には以下の関係があるからです.
まとめると,不偏分散の計算式は不偏性を担保しているものの,それに基づく標準偏差は不偏性を担保できない.なぜなら分散と標準偏差が一次の関係ではないため分布が変わるから.というところです.
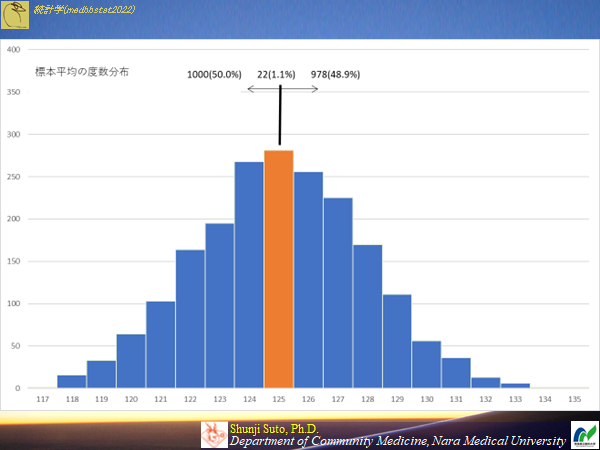
推定の話のキモは「点推定はまず当たらない」というところでしょう.記述統計の場合は当然100%当たる話(事実なので当然)ですから,その続きで推定の話を聞いても受講者は記述統計のイメージを引きずりがちと思います.故に最近は,点推定は当たらないということを意識して伝えています.参考までに母平均の推定も上記のデータセットで行っていますが,僅か1.1%しかあたらなかったという結果です.
あと分散の話では,不偏分散(n-1で除する)と分散(nで除する)とどう使い分けするのか?という話もあります.統計学のオンラインフォローで,そのような質問が出ておりました,そちらはこちらのページ*1に私見を載せています
一連の話にご興味のある方は,以下の資料をご覧いただけたらと思います.
統計学2023(統計の復習用)
https://medbb.net/education/medbbstat2023/index.php
EXCELで発生する誤差および回避する方法について(有効桁数大切という話だけど私もexcelも一緒と判定したのに)
EXCELで計算を行っていると,誤差が知らぬ間に発生している事ないですか?
先日,そのような事象に遭遇して焦ったもので解決法含め示しておきます.
統計学2023(統計の復習用)
https://medbb.net/education/medbbstat2023/index.php
というオンライン講義を年末年始にかけて行っていますが,その時に以下の例題の部分で提供したcsvデータをエクセルで計算しながら解説したのですが,受講生の方が自身でエクセルを使った結果と違うことを教えていただきました.
それは私がaverage関数で平均を求めていたのですが,受講生の方は平均値を手打ちしていたところの違いに起因するものでした.
以下のリンク先のページ内にあるcsvファイルがその時に用いていたものです
例題1-3)(統計学(1)尺度と度数-統計学2023(統計の復習用))
https://medbb.net/education/medbbstat2023/index.php#1-3
真ん中あたりに
medbbstat2023-0101.csv
のリンクがありますので,ご自身で確認される方は,そちらからダウンロードしてください
さて,このデータを使いまわしして以下の例題に取り組んでもらいました
例題2-3)
あるクラスの生徒の身長について
a)この集団の分散を求めよ
b)この集団の標準偏差を求めよ
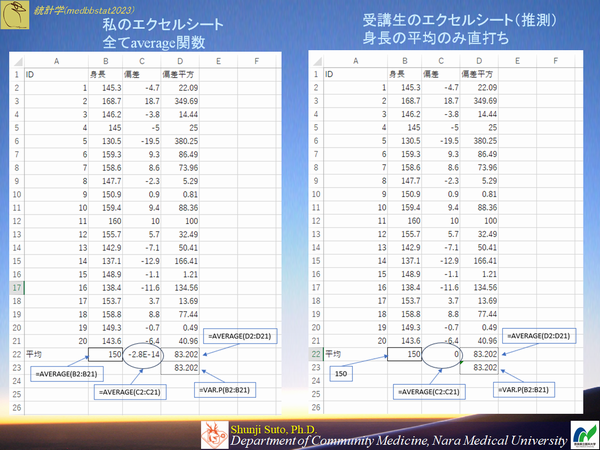
下図の左側が私が解説で作成したシート 右側が受講生の方が仰った内容を基に作成した想定シート.違うところはB22セルのみです.
喋りながら偏差の和が0にならないのはおかしいことと触れておりましたが,誤差だろうと思っていましたが,件のB22セルを直打ちすると0になって驚きました
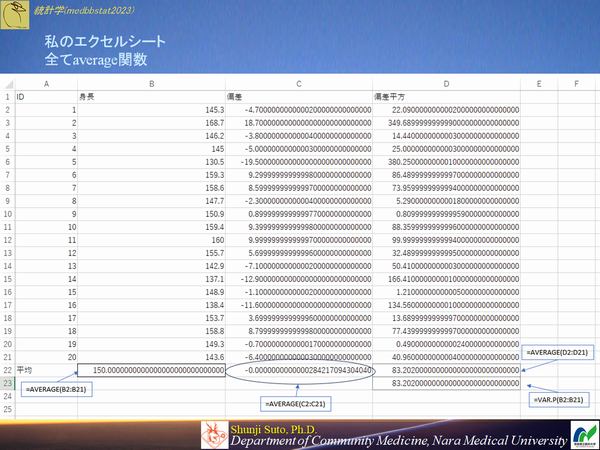
ならばaverage関数で求めたB22セルの平均値に問題があるのだろうと桁数を拡げてみてみると150.0000000000000000000000000000 となっています
これで違うなんで・・・と腑に落ちないのですが,果たして150と同値ではないのでしょうか?
そこで,=IF('私のエクセルシート'!B22='受講者のエクセルシート'!B22,1,0)
と検証したら一緒(1)という結果が返ってきました.!!
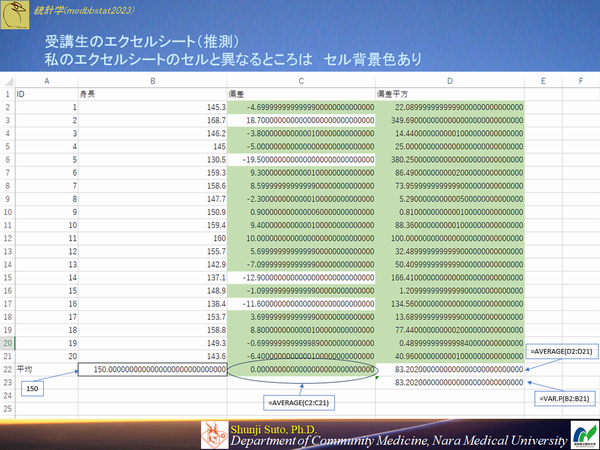
ということで両者のセルがどの程度同値と判定されているのか比較しました
最終的に求めた分散(D22セル)に関しては一緒という恰好でした.
いずれにしても一目どころかエクセル自身も判断できないややこしい問題です
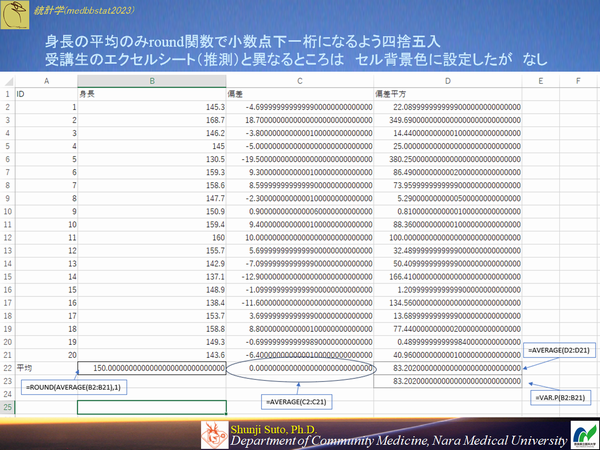
解決策としては,測定値については有効桁数に基づき処理してから計算するのが妥当と思います.今回の場合は有効桁数4桁になりますので,今回は身長のデータですので全て小数点下一桁迄が有効.身長の平均の部分だけround関数で処理しました.
有効桁数の大切さを再認識した一日でした.
セルの絶対参照,相対参照(エクセル)
その昔,アルバイトでパソコンインストラクターをしていた時期がありました.e-Japan戦略の一環として行われていたIT講習会では大阪府吹田市の会場で春先から夏まで沢山喋らせていただきました.もともと講習会の本の作成お手伝い迄の予定でしたが(学生としての本分を全うしないといけないので),予定していたインストラクターの引き抜きがあったらしく人手が足りずで,期間限定で良い経験をしました.受講したご婦人が講習の合間にペイントで私の似顔絵を描いてくれたり,参加者からお褒めの言葉をもらったり,講習会の本にサインを求められたり.受講生が会場近くのビール工場のお祭りにお昼休み中に行ってご機嫌になっていたり・・・,20年以上前の昔話ですが
さて,本題ですが当時,通常のエクセルの授業においてはセルの絶対参照,相対参照が一つのヤマだ! と当時のインストラクターが仰っていたように思います.$マークをつけたら動かなくなるということで理解し使える方もいましたが,どの部分が相対参照だといいのか整理できていないと結局使えないわけでして.
困っていた学生さんに授業後以下のように説明したところわかりやすかったようで喜んでいただいたので以下.
カイ二乗検定を行うときやカッパ統計量を求めるときに必要となります期待値.周辺度数を用いて計算するわけですが,数式を一つ作って後コピーでOKならば間違えることなく計算できます.
例えば下のように観察者A,Bがそれぞれ同じ文章を読みどの季節なのか分類したとしましょう.(1-春 2-夏 3-秋 4-冬)

期待値を求めるわけですが,観察者Aも観察者Bもともに1-春 と分類した文章は周辺度数から求めると,観察者Aが1と答えた合計の度数(586)に対して観察者Bが合計の度数よりどの程度の確率で1と答えるかの確率を乗じたもので求めることが出来ます.
計算式は 586×(565/2284) となります.(以降カッコは無くても結果は一緒なので,586×565/2284と表記します)
エクセルの場合は直接数字を入力せずにその数値が入っているセル番地を指定することで,打ち間違えを防止できますから,今回もセル番地で式を入れようと思います.
そうすると計算式は =I12*M8/M12 となりました.
(列見出し行見出しは以下参考に,表示している一番上は6行目になります)
(観察者AもBも1-春の結果が入るセルはI8セルになります)
G H I J K L M

エクセルの数式はコピーできるものの基本は相対参照でコピーしたセルが元の場所から動いた分だけセル番地を変えてしまいます.便利な反面動いてほしくないのもありますのでその場合絶対参照で指定(F4キー,もしくは直接$マークを入力)します.
灰色で示したI8セルの数式ですが,上述の =I12*M8/M12 のままではなく =I$12*$M8/$M$12 としておけば 観察者Aと観察者Bの組み合わせのセルにコピーすると計算結果を記してくれます.
という恰好で授業をした後に,なんでそのような数式になるの?どうしたら自分でその数式を立てれるようになるのかと,質問を受けました.この授業がエクセル入門的な授業ならば元インストラクターとしてみっちり時間をとるのですが,込み入った統計学の授業だったもので,個別対応となった次第です.
<絶対参照相対参照の入り混じった数式の立て方の説明>
1)まず最初にコピーすることを意識せず,数式をセル番地で作成してください.
2)次にその式を使いまわし(コピー)するのは行方向(縦)列方向(横)のいずれなのみなのか,表のように両方なのか確認してください.
3)1)で記した数式を書いたセルの使いまわしをする方向の直近のセルに,1)と同様に数式をセル番地で作成してください.表のように両方向の場合は両方向に作成してください.
下の例は表を意識して列側行側両方向に数式を作成しています.

4)1)で作った数式と3)で作った数式を比較してください.その中で変化しているセル番地があれば,それは相対参照のまま,変化していないセル番地は絶対参照にしてください
オリジナルの =I12*M8/M12 (セル番地I8 観察者Aが1 観察者Bも1 灰色セル)
最初のI12の列のIは右のセル(セル番地J8)ではJとなっています.下のセル(I9セル)ではIのままですが,動いていたらOKなので最初のIは相対参照.次にI12の行の12は右のセルも下のセルでも12のままです.動いていないので絶対参照になります.
そのようにまとめると下記のように赤字の部分が変化の無かった部分(絶対参照にする部分)になります.

赤い部分の前に$マークを付けると
=I$12*$M8/$M$12
となります.
件の学生は上記の説明で理解し喜んでいたので,参考になればと思いまとめました.
【調べてみました】通巻号数をどのように表記しているのだろう
雑誌であったりミニコミ誌などの発刊番号ですが,私の中では日本語の巻=Vol. 号=No. という感覚で通巻の場合は号数だからNo.を使うんだろうと思っています.
ところがVol.とするのが一般的と言われたことがあったので,大学が発行している広報誌のデータから実際の所を調べようと思った次第です.偏らないように 都道府県毎に2校選び広報誌の表紙の番号表記を調べてまとめました.原則として国立大学法人+公立大学法人の2校とし各都道府県均等に2点に配分する格好で集計しました.なお,どの広報誌も巻号表記ではなく通巻号の格好でした.(シーケンシャルに番号がふられている)
なお,国公立で広報誌が見当たらない場合もありましたのでその時は私学も対象としましたが1県だけ,どうしても2校探すことが出来ませんでした.ですのでスコアの合計は46*2+1=93となっています.
集計したものを円グラフにしたものが以下になります

結果としては確かにVol.を使っているケースが多かったのですが絶対的なものでもないなという印象です.大学の中で用法が異なるケースもいくらかありました.(ですのでスコアは同一大学で1点に収まるように配分しました).
医学部医学科に入学された学生や保護者の方が戸惑うかもしれないこと(2022年度版)
以下,これまでに学生(受験生含む)やその保護者の方と接してきて,なんとなくお伝えしたほうが良いかなと思う部分を取りまとめました.
1)中等教育と高等教育の接続の話
初等中等教育と高等教育との接続の改善について (答申) において以下の記述がある.
初等中等教育と高等教育との接続の改善について (答申) (中央教育審議会 文部科学省)
- 初期中等教育は,「自ら学び,自ら考える力」などの『生きる力』の育成」
- 高等教育は,「主体的に変化に対応し,自ら将来の課題を探求し,その課題に対して幅広い視野から柔軟かつ総合的な判断を下すことのできる力(課題探求能力)の育成」
後期中等教育(高校)は多様で,だれもが同じ格好で高等教育に接続できているか定かではありません.大学に入学するには選抜入試(試験問題)でパフォーマンスを発揮しなくてはなりませんが,そこでは正解の一意性が担保されている世界です.

社会の中では妥当な選択(≒正解)が常に一意性を持つのか定かではありません.ベースとなる知識の獲得度合いを大学入試で図っているとすれば,入学後はその知識を状況に合わせて展開させることが出来るかが問われます.故に,学習スタイルが中等教育までの延長線上で良いはずがないのですが,大学入試の成功体験の影響に思いますが,それまでのスタイルを変えずに押し通そうとする学生さんが一定数存在しているのではないかと思っています.特に情報を詰め込むことで中等教育を乗り切った方は,自身の知識として整理することを日ごろから意識しておかないと,いずれよろしくない状況に陥ると思っています.
以下は,入学された学生さんに実際にお話ししている内容です.
教養教育の目的は知の日常化
— めどぶぶ (@medbb) 2016年4月5日
(よりよい医療に貢献する医療情報技師の役割 より)
<参考>
取り上げた報告書は,上記リンクの中の ●調査室報告書シンポジウム2020報告書(14MB)になります
2)将来に関して医学生の認識の怪しそうな部分(キャリア形成)
帰属意識といえば一般的には会社に対するものなど運営母体に対して持つ形が想定されるように思います.しかしながら医療専門職は専門領域に対する意識が運営組織に対するものより大きいように思います.特に医師の場合は医局という専門職集団に帰属することによりキャリア形成を鑑みた上で医療機関への派遣(入職)が行われてきました.
医局については,「何?」「病院の詰所のこと?」「大学の○○講座のこと=医局?」などフワッとした感じで理解している方も多いように思いますし,私自身関わるまで良く分かっていなかった部分です.大学の講座には教授をはじめとする教員および大学院生などが所属しており,附属病院では講座と対応する診療科で講座教員のほかに診療科所属の医師(医員など)が勤務しています.医局(専門職集団)に所属する医師のことを医局員と呼ぶようです.

「医局人事」と聞くと定年退職するまで人事を握られているのではないかと思われそうですが,そのような人事は卒後15年~20年まででその後は管理職として運営組織への帰属にシフトしていくような格好となっています.私の良く知る例を思い出すと概ね40歳までに医局人事による異動は終わり,その後は開業や医療機関の管理職として組織の運営に携わる格好になっていました.そのため定年退職まで一つの医療機関に勤務するというケースは無い(だろうと思いますが ありえるのかな?)
以上の事から勤務医の平均勤続年数は他業種より短くなりますが,給与水準が他業種よりも高く退職金などについて著しく不利ということでも無いようです.
<参考資料>
3)最近の大学生の学修に関する傾向
大学生がどのように学修しているのか,保護者の方も大学教員も自身の感覚とは異なるところがあり,測りかねる部分もあるように思います.逆に学生は保護者や教員の感覚や意図を理解できない部分があるように思います.教員と保護者の視点で読み解いてみました.経年変化2008→16年を中心にみています.
<教員>
- グループワークなどの場での発言が以前よりも活発な傾向
- 授業の復習は以前よりする傾向(予習はあまり変わらないが)
- 興味を持ったことについて深めていく傾向が減少
- 自由な選択より系統立てて学びたい傾向
- 興味よりも楽に単位を取れる科目を好む傾向
- 知識や技能が身につかないのは大学の責任と思う人が増加傾向(割合は低いが)
- 学修方法そのものを教えてほしい傾向が増加
経験上頷ける部分もあるという印象です.単位の取得が楽な方向になるのは,学生自分を振り返るとなんとも言えませんが,「楽」から「楽しく」になるような努力をしていくことで系統立てて学ぶことだけではく,探求することについて関心を持ってもらえればと思いました.
<保護者>
- 困りごとがあると保護者が助けてくれる恰好(小中学生の頃に保護者が助ける格好だと,傾向が強くなる)
- 保護者のアドバイスを聞きいれる傾向
- 進路などは保護者の意見を重視する傾向(割合は低いが)
幼いころは保護者がある程度手助けしないとなりませんが,その関係性は変わりにくいのかもしれません.以前より社会生活の中で様々な脅威が迫っているように思いますし,そこからご子息を守ることを第一に考えると,この傾向は当然の事にも思います.2022年4月1日から成年年齢は18歳となりました.大学教育の中で成人としての自覚を促す必要も感じています.この点は特に教員が寄り添うにも立ち入れない部分が出てくると思いますので,保護者の皆様と連携しながら社会で活躍できる学生の育成に繋がればと思っております.どうぞよろしくお願いいたします.
<用いた調査報告書>
入学された皆さんへ(2022年度版)
ご入学おめでとうございます.これまでと違い入学したら年齢の異なる方が多いと思っている方が多いのではないでしょうか.年齢が違う同級生にどのように話しかけたら良いのやらと悩む方も多いかと思います.それも一つの経験ですし,学生時代の友人・知人は貴重ですので幅広く多くの方と良い人間関係を築いていただけたら良いなと思っています.良い人間関係の構築には程よい距離感を保つことがカギかなと思っています.あまり近すぎても駄目な場合もあるでしょうし,かといって遠すぎると見失ってしまいかねません.これから本学での6年間の学修が始まりますが,人間関係と同様に様々な事柄に取り組むわけですが得手不得手があったとしても,そのような科目を遠ざけてしまうということはしないでください.
皆さんは医療機関における実習が必要なので講義で学ぶことと,実習で学ぶことが入り乱れる格好になります.講義を疎かにしていると実習で学べるはずのことに気がつかないまま・・・なんてことになりかねません.
(よりよい医療に貢献する医療情報技師の役割 より)
無論,実習も真摯に取り組むことで過去の講義において理解が足りなかった部分に気がつく経験もされると思います.講義だけ,もしくは実習だけ本気出せば済むような世界では無いのでどちらもバランスよく取り組んでください.
講義と実習で経験した「気づき」体験がこれからの人生を豊かにするだろうと思います.残念ながら世の中は学生時代に得た知識だけでは通用しません.国立大学協会「高等教育における国立大学の将来像(最終まとめ)」においても「これからの時代に求められるのは、個々の能力・適性に合った専門的な知識とともに、幅広い分野や考え方を俯瞰して、自らの判断をまとめ表現する力を備えた人材である。」とされており,「気づき」を活かして最良な判断が出来る人になって欲しいという思いです.
「気づき」は自力で気づけるようになれば一番良いのですが,教員などからヒントを出されて気づくというケースが多くなるかなと思います.最悪なのは同期や先輩から「気づき」の機会を奪った格好で答えを教えてもらうこと(=気づいていない)でしょうか.特に初年次の教養で学修するはずの幅広い分野の知識や考え方を疎かにすると専門分野での理解も不十分なものになり,結果的に多くの場面で気がつかない勿体ない人生になりかねません.某名探偵(見た目は子ども頭脳は大人)は自身の立ち位置を理解し,上手く振舞いながら幅広い視点から様々なことに気づいて問題解決しているわけでして.
さて,これまでの短期的な目標に向かっていた学習から,目的を達成するための学修にステージが変わります.第一歩となる一年次を新たな気持ちで歩んでください.
クリスマスケーキ(大阪赤十字看護専門学校の閉校に寄せて)
以下は大阪赤十字看護専門学校の閉校記念誌に寄稿したものです.原稿の締切は2021年12月末でした.
学校とのご縁は大阪府看護教員養成講座の謝恩会で松近先生にお声をかけていただいたのがキッカケになります.トントン拍子に話が進み,その場で情報科学の講師を内諾しました.そこから10年以上の長きに渡りお世話になりました.
授業では行儀良い学生も多かったのですが,一方で私の似顔絵を描くなど自由な学生もおられました.でも謝恩会でお会いすると皆さん立ち振る舞いなど立派に成長されておられ,明るい未来を思わせるものでした.
さて,授業は毎年春から夏にかけての時期でしたのでクリスマスと関係ないのですが,この原稿はクリスマスイブが締め切り.学校のことを振り返ろうとするとジングルベルとケーキが頭の中をよぎります.
当時の私は結婚4年目で3人家族の大学院生.大変な状況を察した松近先生はクリスマスにケーキをプレゼントしてくださいました.子どもと一緒にケーキを頂戴するためにこの時期は学校にお邪魔していました.その後子ども増えましたが毎年変わることなく皆で先生にご挨拶.楽しい想い出となっています.
クリスマスケーキはその時に楽しんで終わるものではなく,折に触れ振り返ることができる想い出が詰まったものです.大阪赤十字看護専門学校も養成機関としての使命を終えますが,偶然卒業生の方とお会いして想い出話に花咲かせるだけでなく,新たなご縁に繋がったこともありました.
これまでありがとう,これからもよろしく.